题目内容
7.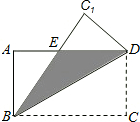 如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.
如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.(1)求证:△ABE≌△C1DE;
(2)求图中阴影部分的面积.
分析 (1)由矩形的性质和翻折的性质可知∠A=∠C1,AB=C1D,依据AAS可证明△ABE≌△C1DE;
(2)由全等三角形的性质可知:BE=ED,设DE=BE=x,则AE=4-x,在Rt△AEB中,利用勾股定理列出关于x的方程求解即可.
解答 解:(1)∵四边形ABCD为矩形,
∴AB=DC,∠A=∠C=90°.
由翻折的性质可知:∠C1=∠C,C1D=DC.
∴∠A=∠C1,AB=C1D.
在△ABE和△C1DE中,$\left\{\begin{array}{l}{∠A=∠{C}_{1}}\\{∠AEB=∠{C}_{1}ED}\\{AB={C}_{1}D}\end{array}\right.$,
∴△ABE≌△C1DE.
(2)∵△ABE≌△C1DE,
∴BE=ED.
设DE=BE=x,则AE=4-x.
在Rt△AEB中,由勾股定理可知:BE2=AB2+AE2,即x2=32+(4-x)2,解得:x=$\frac{25}{8}$
S△EDB=$\frac{1}{2}$AB•DE=$\frac{1}{2}×$3×$\frac{25}{8}$=$\frac{75}{16}$.
点评 本题主要考查的翻折的性质、矩形的性质、全等三角形的性质和判定、勾股定理的应用,在Rt△AEB中,利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.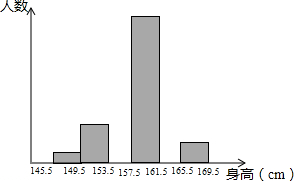 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
| 组别 | 人数 | 百分比 |
| 145.5~149.5 | 1 | 2% |
| 149.5~153.5 | 4 | 8% |
| 153.5~157.5 | m | 40% |
| 157.5~161.5 | 15 | 30% |
| 161.5~165.5 | 8 | n |
| 165.5~169.5 | 2 | 4% |
| 合计 | 50 | 100% |
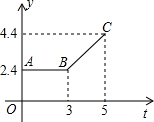 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.