题目内容
16.($\frac{1}{2}$x-$\frac{1}{3}$y)2+$\frac{2}{3}$xy=($\frac{1}{2}$x+$\frac{1}{3}$y)2.分析 利用完全平方公式,即可解答.
解答 解:∵$(\frac{1}{2}x-\frac{1}{3}y)^{2}=\frac{1}{4}{x}^{2}-\frac{1}{3}xy+\frac{1}{9}{y}^{2}$,$(\frac{1}{2}x+\frac{1}{3}y)^{2}=\frac{1}{4}{x}^{2}+\frac{1}{3}xy+\frac{1}{9}{y}^{2}$,
∴$(\frac{1}{2}x-\frac{1}{3}y)^{2}+\frac{2}{3}xy=(\frac{1}{2}x+\frac{1}{3}y)^{2}$,
故答案为:$\frac{2}{3}$xy.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.

练习册系列答案
相关题目
 如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:
如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论: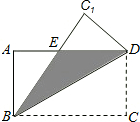 如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.
如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.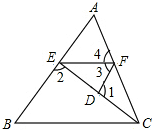 如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.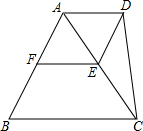 如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.
如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.