题目内容
15. 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
分析 如图过点C作CH⊥AB于H,延长HC交⊙C于P′.点P与P′重合时,△PAB的面积最大,求出P′H、AB的值即可解决问题.
解答 解:如图过点C作CH⊥AB于H,延长HC交⊙C于P′.
∵直线AB的解析式为y=$\frac{4}{3}$x-4,
∴直线CH的解析式为y=-$\frac{3}{4}$x+1,
由$\left\{\begin{array}{l}{y=\frac{4}{3}x-4}\\{y=-\frac{4}{3}x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=-\frac{4}{5}}\end{array}\right.$,
∴H($\frac{12}{5}$,-$\frac{4}{5}$),
∴CH=$\sqrt{(\frac{12}{5})^{2}+(\frac{9}{5})^{2}}$=3,P′H=3+1=4,
∵A(5,0),B(0,-4),
∴AB=5,
∵点P与P′重合时,△PAB的面积最大,
∴△PAB面积的最大值为$\frac{1}{2}$×5×4=10,
故选A.
点评 本题考查一次函数图象上点的特征、点与圆的位置关系等知识,解题的关键是学会添加常用辅助线,正确寻找点P的位置确定最大值,属于中考常考题型.

练习册系列答案
相关题目
5.一个多边形的每一个外角都等于120°,则这个多边形的边数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

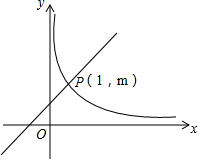 如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).
如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).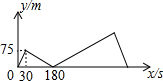 A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.
A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.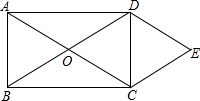 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD. 已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )
已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )