题目内容
7.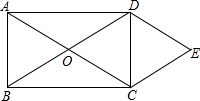 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形.
(2)如果△DEC为等边三角形,求矩形长和宽的比是多少.
分析 (1)首先证明四边形OCED是平行四边形,再证明OD=OC即可解决问题;
(2)只要证明△ODC是等边三角形即可解决问题;
解答 (1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴OD=OB=OC=OA,
∴四边形OCED是菱形.
(2)解:∵△CDE是等边三角形,四边形OCED是菱形,
∴CE=DE=DC=OD=OC,
∴△ODC是等边三角形,
∴∠BDC=60°,
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴$\frac{BC}{CD}$=tan60°=$\sqrt{3}$,
∴矩形长和宽的比是$\sqrt{3}$.
点评 本题考查矩形的性质、菱形的判定和性质、等边三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.若$\sqrt{x-2}$+$\root{3}{4-x}$有意义,则x的取值范围是( )
| A. | x≥2 | B. | 2≤x≤4 | C. | x<4 | D. | 2<x<4 |
15. 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
16.下列计算中正确的是( )
| A. | 2a-a=2 | B. | -1-2=1 | C. | (-a2)3=a6 | D. | -a-2=-$\frac{1}{{a}^{2}}$ |
17.若把分式$\frac{x+y}{xy}$中的x和y都扩大3倍,那么分式的值( )
| A. | 为原来的3倍 | B. | 不变 | C. | 为原来的$\frac{1}{3}$ | D. | 为原来的$\frac{1}{6}$ |
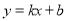 (
(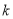 、
、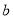 为常数,
为常数, 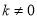 )图象如图所示,则关于
)图象如图所示,则关于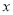 的不等式
的不等式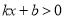 的解集为( )
的解集为( )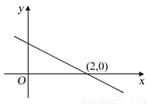
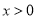 B.
B. 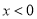 C.
C. 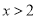 D.
D. 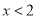
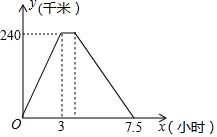 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.
小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示. 如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少?
如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少? 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=45°,则∠ADB=105°.
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=45°,则∠ADB=105°.