题目内容
3.菱形ABCD的周长是20,对角线AC、BD相交于点O,若BD=6,则菱形ABCD的面积是24.分析 根据菱形的周长可以计算菱形的边长,菱形的对角线互相垂直平分,已知AB,AO根据勾股定理即可求得BO的值,根据对角线长即可计算菱形ABCD的面积.
解答 解:菱形周长为20,则AB=5,
菱形对角线互相垂直平分,
∴AO=3,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=4,
∴BD=2BO=8,
故菱形ABCD的面积为$\frac{1}{2}$×6×8=24.
故答案为24.
点评 本题考查了菱形对角线互相垂直平分的性质,注意菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求BO的值是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.若$\sqrt{x-2}$+$\root{3}{4-x}$有意义,则x的取值范围是( )
| A. | x≥2 | B. | 2≤x≤4 | C. | x<4 | D. | 2<x<4 |
15. 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
13.若m>n,下列不等式不一定成立的是( )
| A. | m2>n2 | B. | m+2>n+2 | C. | $\frac{m}{2}$>$\frac{n}{2}$ | D. | -2m<-2n |
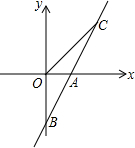 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2). 如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少?
如图,O是菱形ABCD一条对角线BD上的一个点,它是菱形一边AB的距离(OE)是2cm,那么O到BC的距离是多少?