题目内容
10.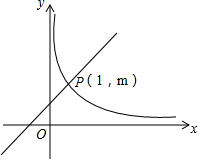 如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).
如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于P(1,m).(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q((2,1));
(3)若过P、Q两点的抛物线与y轴的交点为N(0,$\frac{5}{3}$),求该抛物线的解析式,并求出抛物线的对称轴方程.
分析 (1)直接将P点代入反比例函数解析式得出m的值,进而把P点代入一次函数解析式得出答案;
(2)利用全等三角形的判定和性质得出△APO≌△BQO(AAS),即可得出Q点坐标;
(3)直接利用待定系数法求出二次函数解析式进而得出答案.
解答 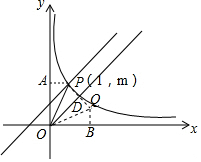 解:(1)把P(1,m)代入y=$\frac{2}{x}$,得m=2,
解:(1)把P(1,m)代入y=$\frac{2}{x}$,得m=2,
∴P(1,2)
把(1,2)代入y=kx+1,得k=1;
(2)如图所示:过点P作PA⊥y轴于点A,过点Q作QB⊥x轴于点B,
∵点Q与点P关于y=x成轴对称,OP=OQ,
∴∠POD=∠DOQ,∠AOD=∠BOD=45°,
∴∠AOP=∠BOQ,
在△APO和△BQO中,
$\left\{\begin{array}{l}{∠PAO=∠QBO}\\{∠AOP=∠BOQ}\\{PO=QO}\end{array}\right.$,
∴△APO≌△BQO(AAS),
∴AO=OB=2,AP=QB=1,
∴Q点的坐标为:(2,1).
故答案为:(2,1);
(3)设抛物线的解析式为y=ax2+bx+c,得:
$\left\{\begin{array}{l}{a+b+c=2}\\{4a+2b+c=1}\\{c=\frac{5}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=1}\\{c=\frac{5}{3}}\end{array}\right.$,
故抛物线解析式为:y=-$\frac{2}{3}$x2+x+$\frac{5}{3}$,
则对称轴方程为x=-$\frac{1}{-\frac{2}{3}}$=$\frac{3}{2}$.
点评 此题主要考查了待定系数法求一次函数以及二次函数解析式、全等三角形的判定与性质等知识,正确利用y=x的特殊性求出△APO≌△BQO是解题关键.

| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 菱形 |
| A. | x≥2 | B. | 2≤x≤4 | C. | x<4 | D. | 2<x<4 |
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
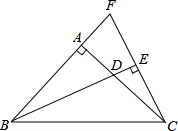 如图,在△ABC中,∠BAC=90°,AB=AC,D为AC边上一点,作EC⊥BD于E,交BA的延长线于F,则有( )
如图,在△ABC中,∠BAC=90°,AB=AC,D为AC边上一点,作EC⊥BD于E,交BA的延长线于F,则有( )| A. | △ABD≌△ACF | B. | △BEF≌△CAF | C. | △BEC≌△BEF | D. | △ABD≌△EBC |
 的解x、y满足x+y>0,求m的取值范围.
的解x、y满足x+y>0,求m的取值范围.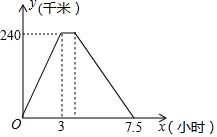 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.
小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示. 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=45°,则∠ADB=105°.
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=45°,则∠ADB=105°.