题目内容
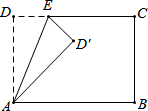 如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′.
如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′.(1)求点D′刚好落在对角线AC上时,线段D′C的长;
(2)求点D′刚好落在线段BC的垂直平分线上时,DE的长;
(3)求点D′刚好落在线段AB的垂直平分线上时,DE的长.
考点:翻折变换(折叠问题),线段垂直平分线的性质,勾股定理
专题:
分析:(1)如图1,求出AC的长度,即可解决问题.
(2)如图2,证明D′D=AD′=AD,此为解决问题的关键性结论;运用勾股定理即可解决问题.
(3)如图3或4,类比(2)中的解法,借助勾股定理,即可解决问题.
(2)如图2,证明D′D=AD′=AD,此为解决问题的关键性结论;运用勾股定理即可解决问题.
(3)如图3或4,类比(2)中的解法,借助勾股定理,即可解决问题.
解答: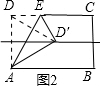

 解:(1)如图1,
解:(1)如图1,
∵四边形ABCD为矩形,
∴∠B=90°,BC=AD=5,由勾股定理求得AC=
;
∵点A、D′、C在同一直线上,
∴D′C=AC-AD′=AC-AD=
-5.
(2)如图2,连接D′D,
∵点D′在BC的垂直平分线上,
∴点D′在AD的垂直平分线上,
∴D′D=AD′=AD;
设DE为x,易得AE=2x,
由勾股定理得:(2x)2-x2=52,
∴x=
.
(3)分两种情况讨论:
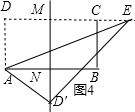
①当点D′在矩形内部时,如图3,连接D′B,
∵点D′在AB的垂直平分线上,
∴AN=4;
∵AD′=5,由勾股定理得D′N=3,
∴D′M=2;设DE为y,
∴EM=4-y,D′E=y;
在△EMD′中,由勾股定理得:y2=(4-y)2+22,
∴y=
,即DE的长为
.
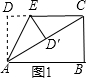
②当点D′在矩形外部时,如图4,连接D′B,
同①的方法可得D′N=3,
∴D′M=8,设DE为z,
∴EM=z-4,D′E=z,
在△EMD′中,由勾股定理得:z2=(z-4)2+82,
∴z=10,即DE的长为10.
综上所述,点D′刚好落在线段AB的垂直平分线上时,DE的长为
或10



 解:(1)如图1,
解:(1)如图1,∵四边形ABCD为矩形,
∴∠B=90°,BC=AD=5,由勾股定理求得AC=
| 89 |
∵点A、D′、C在同一直线上,
∴D′C=AC-AD′=AC-AD=
| 89 |
(2)如图2,连接D′D,
∵点D′在BC的垂直平分线上,
∴点D′在AD的垂直平分线上,
∴D′D=AD′=AD;
设DE为x,易得AE=2x,
由勾股定理得:(2x)2-x2=52,
∴x=
| 5 |
| 3 |
| 3 |
(3)分两种情况讨论:
①当点D′在矩形内部时,如图3,连接D′B,
∵点D′在AB的垂直平分线上,
∴AN=4;
∵AD′=5,由勾股定理得D′N=3,
∴D′M=2;设DE为y,
∴EM=4-y,D′E=y;
在△EMD′中,由勾股定理得:y2=(4-y)2+22,
∴y=
| 5 |
| 2 |
| 5 |
| 2 |
②当点D′在矩形外部时,如图4,连接D′B,
同①的方法可得D′N=3,
∴D′M=8,设DE为z,
∴EM=z-4,D′E=z,
在△EMD′中,由勾股定理得:z2=(z-4)2+82,
∴z=10,即DE的长为10.
综上所述,点D′刚好落在线段AB的垂直平分线上时,DE的长为
| 5 |
| 2 |
点评:该题以矩形为载体,以翻折变换为方法,以考查矩形的性质、翻折变换的性质、勾股定理等几何知识点为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
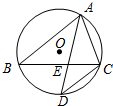 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD. 如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是
如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是