题目内容
15.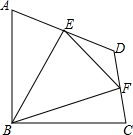 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
分析 连接AC,由S△ABC=$\frac{1}{2}$•BC•AB=$\frac{1}{2}$$•2\sqrt{2}$$•2\sqrt{2}$=4,可得S△ADC=6-4=2,根据S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED易知S△ABE+S△BCF=$\frac{1}{2}$S四边形ABCD=3,S△EDF=$\frac{1}{2}$,由此即可解决问题.
解答 解:连接AC.∵S△ABC=$\frac{1}{2}$•BC•AB=$\frac{1}{2}$$•2\sqrt{2}$$•2\sqrt{2}$=4,
∵四边形ABCD的面积为6,
∴S△ADC=6-4=2,
∵S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED,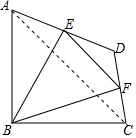
易知S△ABE+S△BCF=$\frac{1}{2}$S四边形ABCD=3,S△EDF=$\frac{1}{2}$,
∴S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED=6-3-$\frac{1}{2}$=$\frac{5}{2}$.
点评 本题考查三角形中位线定理、等腰直角三角形的性质,四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.2015年日照市人民政府投入1000万元用于改造乡村小学班班通工程建设,计划到2017年再追加投资210万元,如果每年的平均增长率相同,那么我市这两年该项投入的平均增长率为( )
| A. | 1.21% | B. | 8% | C. | 10% | D. | 12.1% |
5.位于武侯区“中国女鞋之都”的某制鞋企业为了了解初中学生穿鞋的尺码情况,选择对某校的40名女生进行了调查,结果如下表所示,那么在平均数、中位数、众数三个统计量中,该制鞋企业最感兴趣的统计量是众数,该统计量的数值是36码.
| 尺码(单位:码) | 33 | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 8 | 8 | 14 | 6 | 2 |
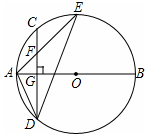 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
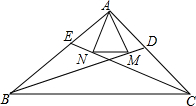 在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.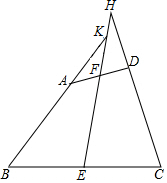 如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.
如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.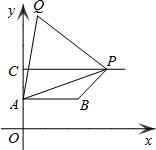 如图,已知点A(0,2)、B(2$\sqrt{3}$,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.
如图,已知点A(0,2)、B(2$\sqrt{3}$,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.