题目内容
8.某项工程限期完成,甲队独做正好按期完成,乙队独做则要误期4天,现两队合做3天后,余下的工程再由乙队独做,比限期提前一天完成.(1)请问该工程限期是多少天?
(2)已知甲队每天的施工费为1000元,乙队每天的施工费为800元,要使该项工程的总费用不超过7000元,乙队最多施工多少天?
分析 (1)设工程的限期是x天,则甲队正好干x天完成任务,则乙队需(x+4)天完成任务,由题意得:甲干3天的工作量+乙干(x-1)天的工作量=1,再根据等量关系列出方程,解方程即可.
(2)可由甲乙两队的工作量之和为1及总费用不超过7000元两个关系进行分析.
解答 解:(1)设工程的限期是x天,由题意得;
$\frac{3}{x}$+$\frac{x-1}{x+4}$=1,
解得:x=6,
经检验:x=6是分式方程的解,
答:工程的限期是6天.
(2)设甲工程队施工a天,乙工程队施工b天时,总的施工费用不超过7000元.
根据题意得:$\frac{a}{6}$+$\frac{b}{10}$=1.
解得:a=6-$\frac{3}{5}$b.
工程费用:1000a+800b≤7000.
即1000(6-$\frac{3}{5}$b)+800b≤7000,
解得b≤5.
答:要使该项工程的总费用不超过7000元,乙队最多施工5天.
点评 此题主要考查了分式方程的应用,关键是弄懂题意,找出题目中的等量关系,此题所用的公式是:工作量=工作效率×工作时间.

练习册系列答案
相关题目
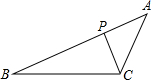 如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).
如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).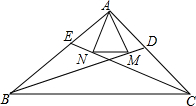 在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.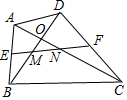 如图.在四边形ABCD中.AC=BD,E,F分别为AB,CD的中点(O,M,N不重合),仔细观察你会发观.无论四边形ABCD的形状如何变化,只要保待对角线相等,则EF与两条对角线围成的三角形总是等腰三角形(图中的△OMN),请说明理由.
如图.在四边形ABCD中.AC=BD,E,F分别为AB,CD的中点(O,M,N不重合),仔细观察你会发观.无论四边形ABCD的形状如何变化,只要保待对角线相等,则EF与两条对角线围成的三角形总是等腰三角形(图中的△OMN),请说明理由.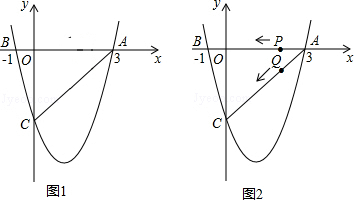
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$.