题目内容
13.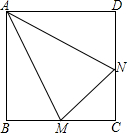 如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.
如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
分析 (1)只要证明△ABM≌△ADN(HL),推出∠BAM=∠DAN,由∠MAN=30°,∠BAD=90°,即可推出∠BAM=30°;
(2)作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,根据$\frac{1}{2}$•AN•MH=1,列出方程即可;
解答 解: (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
∵AM=AN,
在Rt△ABM和Rt△ADN中,
$\left\{\begin{array}{l}{AB=AD}\\{AM=AN}\end{array}\right.$,
∴△ABM≌△ADN(HL),
∴∠BAM=∠DAN,
∵∠MAN=30°,∠BAD=90°,
∴∠BAM=30°.
(2)作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,
∵$\frac{1}{2}$•AN•MH=1,
∴$\frac{1}{2}$•2x•x=1,
解得x=1或-1(舍弃),
∴AB=$\sqrt{3}$BM=$\sqrt{3}$,
∴正方形ABCD的边长为$\sqrt{3}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、直角三角形的30度角的性质、三角形的面积等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
4.2015年日照市人民政府投入1000万元用于改造乡村小学班班通工程建设,计划到2017年再追加投资210万元,如果每年的平均增长率相同,那么我市这两年该项投入的平均增长率为( )
| A. | 1.21% | B. | 8% | C. | 10% | D. | 12.1% |
5.位于武侯区“中国女鞋之都”的某制鞋企业为了了解初中学生穿鞋的尺码情况,选择对某校的40名女生进行了调查,结果如下表所示,那么在平均数、中位数、众数三个统计量中,该制鞋企业最感兴趣的统计量是众数,该统计量的数值是36码.
| 尺码(单位:码) | 33 | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 8 | 8 | 14 | 6 | 2 |
2.已知圆锥侧面展开图的面积为65πcm2,其底面圆半径为5cm,则圆锥的母线长是( )
| A. | 13cm | B. | 12cm | C. | 10cm | D. | 5cm |
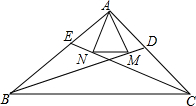 在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$. 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$. 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )