题目内容
 如图,在△ABC中,AB=AC,AB的垂直平分线交BC于D,交AB于G,AC的垂直平分线交BC于E,交AC于F,且BD=DE.
如图,在△ABC中,AB=AC,AB的垂直平分线交BC于D,交AB于G,AC的垂直平分线交BC于E,交AC于F,且BD=DE.求证:∠BAC=120°.
考点:线段垂直平分线的性质,全等三角形的判定与性质,等腰三角形的性质
专题:证明题
分析:连结AD、AE,根据线段垂直平分线的性质得DA=DB,EA=EC,则根据等腰三角形的性质得∠B=∠BAD,∠C=∠CAE,由三角形外角性质得∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,则∠ADE=2∠B,∠AEC=2∠C,由AB=AC得到∠B=∠C,所以∠ADE=∠AED,则AE=AD,加上BD=DE,可判断△ADE为等边三角形,
所以∠ADE=60°,易得∠B=30°,然后根据三角形内角和定理可计算出∠BAC的度数.
所以∠ADE=60°,易得∠B=30°,然后根据三角形内角和定理可计算出∠BAC的度数.
解答:证明:连结AD、AE,如图,

∵DG垂直平分线AB,
∴DA=DB,
∴∠B=∠BAD,
∵EF垂直平分线AC,
∴EA=EC,
∴∠C=∠CAE,
而∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠ADE=2∠B,∠AEC=2∠C,
∵AB=AC,
∴∠B=∠C,
∴∠ADE=∠AED,
∴AE=AD,
∵BD=DE,
∴AD=DE=AE,
∴△ADE为等边三角形,
∴∠ADE=60°,
∴∠B=30°,
∴∠BAC=180°-2×30°=120°.

∵DG垂直平分线AB,
∴DA=DB,
∴∠B=∠BAD,
∵EF垂直平分线AC,
∴EA=EC,
∴∠C=∠CAE,
而∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠ADE=2∠B,∠AEC=2∠C,
∵AB=AC,
∴∠B=∠C,
∴∠ADE=∠AED,
∴AE=AD,
∵BD=DE,
∴AD=DE=AE,
∴△ADE为等边三角形,
∴∠ADE=60°,
∴∠B=30°,
∴∠BAC=180°-2×30°=120°.
点评:本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等.也考查了等腰三角形的性质和等边三角形的判定与性质.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
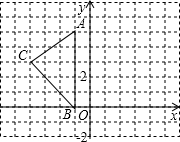 如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3). 如图,AD∥BC,∠A=∠C,BE、DF分别平分∠ABC和∠CDA.求证:BE∥DF.
如图,AD∥BC,∠A=∠C,BE、DF分别平分∠ABC和∠CDA.求证:BE∥DF.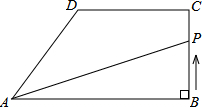 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2). 如图,先将正方形纸片ABCD对折,折痕为EF,再把点C折叠在EF上,折痕为DG,点C在 EF上对应点为P,则∠CPE=
如图,先将正方形纸片ABCD对折,折痕为EF,再把点C折叠在EF上,折痕为DG,点C在 EF上对应点为P,则∠CPE=