题目内容
7. 如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.
如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.(1)求A,B,C的坐标;
(2)求S△ABC;
(3)在x轴上是否得在点P使△PBC为等腰三角形?若存在,直接写出P的坐标,若不存在请说明理由.
分析 (1)解方程求出x和y的值即可求得结论;
(2)根据三角形的面积公式即可求得结论;
(3)存在,根据勾股定理得到BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{2}$,设P(a,0)①当B为顶点时,②当C为顶点时,③当P为顶点时,解方程即可得到结论.
解答 解:(1)y=-x2+1,令y=0,则0=-x2+1,
解得:x1=-1,x2=1,令x=0,则y=1,
∴A(-1,0),B(1,0),C(0,1);
(2)S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×1=1;
(3)存在,
BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{2}$,
设P(a,0)
①当B为顶点时,则|a-1|=$\sqrt{2}$,
解得:a=1±$\sqrt{2}$,
∴P(1+$\sqrt{2}$,0)或P(1-$\sqrt{2}$,0);
②当C为顶点时,即CP=CP,
∵OC⊥PB,
∴OP=OB=1,
∴P(-1,0);
③当P为顶点时,即PC=PB,
∴$\sqrt{{a}^{2}+{1}^{2}}$=|1-a|,
解得:a=0,
∴P(0,0);
综上所述:P的坐标为:P1(1+$\sqrt{2}$,0),P2(1-$\sqrt{2}$,0),P3(-1,0),P4(0,0).
点评 此题是二次函数综合题,主要考查了根据抛物线的解析式的确定点的坐标,抛物线的性质,等腰三角形的性质,解本题的关键是熟练掌握抛物线的性质和等腰三角形的性质,能灵活运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
3.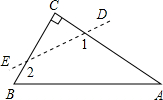 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 150° | D. | 270° |
4.关于x的方程x2+kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
 如图所示:已知△AOB≌△DOC,求证△ABC≌△DCB.
如图所示:已知△AOB≌△DOC,求证△ABC≌△DCB.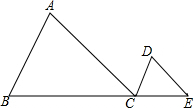 如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.
如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.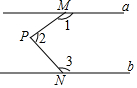 如图,a∥b,M、N分别在直线a、b上,P为两平行线间的一点,则图中∠1,∠2,∠3满足的关系是∠1+∠2+∠3=360°.
如图,a∥b,M、N分别在直线a、b上,P为两平行线间的一点,则图中∠1,∠2,∠3满足的关系是∠1+∠2+∠3=360°.