题目内容
18．试用配方法证明：代数式x2+3x-$\frac{3}{2}$的值不小于-$\frac{15}{4}$．分析 先用配方法把代数式x2+3x-$\frac{3}{2}$化成（x+$\frac{3}{2}$）2-$\frac{15}{4}$的形式，然后利用非负数的性质即可证明．
解答 证明：∵x2+3x-$\frac{3}{2}$=（x+$\frac{3}{2}$）2-$\frac{15}{4}$≥-$\frac{15}{4}$，
∴代数式x2+3x-$\frac{3}{2}$的值不小于-$\frac{15}{4}$．
点评 本题考查了配方法的应用，解题的关键是能够将原来的二次三项式配方成完全平方的形式，难度不大．
练习册系列答案
相关题目
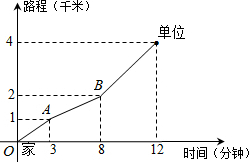王老师从家门口骑车去单位上班，先走平路到达A地，再上坡到达B地，最后下坡到达工作单位，所用的时间与路程的关系如图所示．若王老师下班时，还沿着这条路返回家中，回家途中经过平路、上坡、下坡的速度不变，那么王老师回家需要的时间是15分钟．
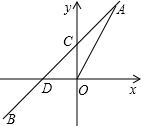如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数图象经过点B（-2，-1），与y轴的交点为C，与x轴的交点为D．
如图，二次函数y=-x2+1与坐标轴交于A、B、C三点．
15．方程x-1=5+2x的解为（ ）
| A． | .x=-2 | B． | x=2 | C． | x=-6 | D． | x=6 |