题目内容
4.关于x的方程x2+kx-1=0的根的情况描述正确的是( )| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
分析 根据方程的系数结合根的判别式可得出△=k2+4>0,由此即可得出无论k为何值,方程都有两个不相等的实数根.
解答 解:△=k2-4×1×(-1)=k2+4.
∵k2≥0,
∴k2+4>0,即△>0,
∴k为任何实数,方程都有两个不相等的实数根.
故选B.
点评 本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
15.方程x-1=5+2x的解为( )
| A. | .x=-2 | B. | x=2 | C. | x=-6 | D. | x=6 |
19.下列根式中,能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{30}$ |
9.已知一个样本1,3,2,x,4的平均数是3,则这个样本的方差是( )
| A. | 2 | B. | 2.5 | C. | 10 | D. | $\frac{6}{5}$ |
16.下列实数最小的是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
13.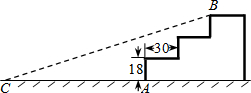 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
 如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.
如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.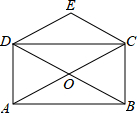 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )