题目内容
3.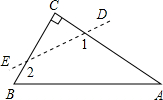 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 150° | D. | 270° |
分析 根据邻补角的定义表示出∠CDE和∠CED,再根据三角形的内角和等于180°列式整理即可得解.
解答 解:∠CDE=180°-∠1,
∠CED=180°-∠2,
在△CDE中,∠CDE+∠CED+∠C=180°,
所以,180°-∠1+180°-∠2+90°=180°,
所以,∠1+∠2=270°.
故选D.
点评 本题考查了三角形的内角和定理,邻补角的定义,难点在于用∠1、∠2表示出三角形的内角.

练习册系列答案
相关题目
8.$\frac{1}{2}$-$\frac{1}{6}$-$\frac{1}{12}$-$\frac{1}{20}$-$\frac{1}{30}$=( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{6}$ |
15.方程x-1=5+2x的解为( )
| A. | .x=-2 | B. | x=2 | C. | x=-6 | D. | x=6 |
13.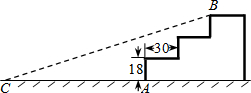 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
 如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.
如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.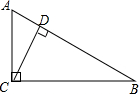 如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
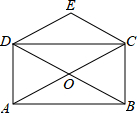 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )