题目内容
15.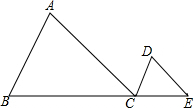 如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.
如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.
分析 根据题目中的条件和三角形的相似,可以求得CE的长.
解答 解:∵∠ACD=∠ABC,
∴∠A=∠DCE,
∵△ABC和△DCE相似,
∴$\frac{AB}{CE}$=$\frac{AC}{CD}$或$\frac{AB}{CD}$=$\frac{AC}{CE}$,即$\frac{6}{CE}$=$\frac{9}{3}$或$\frac{6}{3}$=$\frac{9}{CE}$,
解得,CE=2或4.5,
故答案为:2或4.5.
点评 本题考查相似三角形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用三角形的相似解答.

练习册系列答案
相关题目
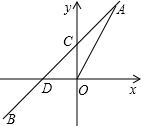 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D. 如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数.
如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数. 如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.
如图,二次函数y=-x2+1与坐标轴交于A、B、C三点.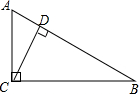 如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.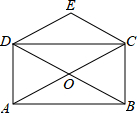 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )