题目内容
4.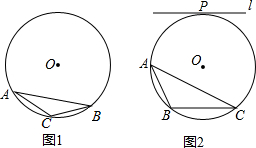 ⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.
分析 (1)过点C作直径CD,由于AC=BC,$\widehat{AC}$=$\widehat{BC}$,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;
(2)连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.
解答 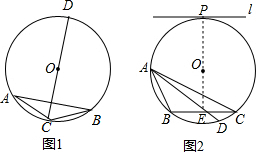 解:(1)如图1,
解:(1)如图1,
直径CD为所求;
(2)如图2,
弦AD为所求.
点评 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的性质.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.把数据167000用科学记数法表示为( )
| A. | 1.67×106 | B. | 1.67×105 | C. | 1.67×104 | D. | 167×103 |
12.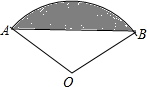 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |
9.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
| A. | a>1 | B. | a≤2 | C. | 1<a≤2 | D. | 1≤a≤2 |
14. 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )| A. | 50° | B. | 20° | C. | 60° | D. | 70° |

 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.