题目内容
1.某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题.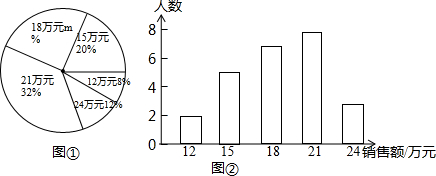
(Ⅰ)该商场服装部营业员的人数为25,图①中m的值为28
(Ⅱ)求统计的这组销售额额数据的平均数、众数和中位数.
分析 (1)根据条形统计图即可得出样本容量根据扇形统计图得出m的值即可;
(2)利用平均数、中位数、众数的定义分别求出即可;
解答 解:(1)根据条形图2+5+7+8+3=25(人),
m=100-20-32-12-8=28;
故答案为:25,28.
(2)观察条形统计图,
∵$\overline{x}=\frac{12×2+15×5+18×7+21×8+24×3}{25}$=18.6,
∴这组数据的平均数是18.6,
∵在这组数据中,21出现了8次,出现的次数最多,
∴这组数据的众数是21,
∵将这组数据按照由小到大的顺序排列,其中处于中间位置的数是18,
∴这组数据的中位数是18.
点评 此题主要考查了平均数、众数、中位数的统计意义以及利用样本估计总体等知识.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
11.甲、乙两班分别由10名选手参加健美比赛,两班参赛选手身高的方差分别是S甲2=1.5,S乙2=2.5,则下列说法正确的是( )
| A. | 甲班选手比乙班选手的身高整齐 | B. | 乙班选手比甲班选手的身高整齐 | ||
| C. | 甲、乙两班选手的身高一样整齐 | D. | 无法确定哪班选手的身高整齐 |
12.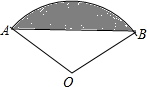 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |
9.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
| A. | a>1 | B. | a≤2 | C. | 1<a≤2 | D. | 1≤a≤2 |
6.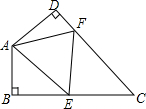 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
11.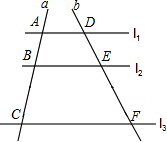 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )| A. | $\frac{8}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 10 |
 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.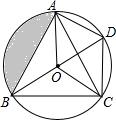 如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.