题目内容
3．（1）计算：（6-π）0+（-$\frac{1}{5}$）-1-3tan30°+|-$\sqrt{3}$|（2）解方程：$\frac{x}{x-2}$-$\frac{2}{{x}^{2}-4}$=1．
分析 （1）原式第一项利用零指数幂法则计算，第二项利用负整数指数幂法则计算，第三项利用特殊角的三角函数值计算，最后一项利用绝对值的代数意义化简，计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=1-5-$\sqrt{3}$+$\sqrt{3}$=-4；
（2）去分母得：x（x+2）-2=（x+2）（x-2），
去括号得：2x=-2，
解得：x=-1．
经检验x=-1是分式方程的解．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
14．把数据167000用科学记数法表示为（ ）
| A． | 1.67×106 | B． | 1.67×105 | C． | 1.67×104 | D． | 167×103 |
11．甲、乙两班分别由10名选手参加健美比赛，两班参赛选手身高的方差分别是S甲2=1.5，S乙2=2.5，则下列说法正确的是（ ）
| A． | 甲班选手比乙班选手的身高整齐 | B． | 乙班选手比甲班选手的身高整齐 | ||
| C． | 甲、乙两班选手的身高一样整齐 | D． | 无法确定哪班选手的身高整齐 |
12．
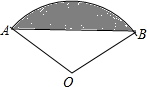如图所示，扇形AOB的圆心角120°，半径为2，则图中阴影部分的面积为（ ）
如图所示，扇形AOB的圆心角120°，半径为2，则图中阴影部分的面积为（ ）| A． | $\frac{4π}{3}$-2$\sqrt{3}$ | B． | $\frac{4π}{3}$-$\sqrt{3}$ | C． | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D． | $\frac{4π}{3}$ |