题目内容
16. 如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7.
如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7.
分析 由条件“AF+CD=AD”可知属于截长补短全等型,故延长CA至点G使GA=CD,连接GB,易知△GBA≌△DAC.结合该全等三角形的对应边相等、等腰三角形的判定得到△BGF为等腰三角形,又有等腰三角形的性质推知AB=AE.设AD=a,则BG=a,BA=AE=a-2,GA=GF-AF=BG-AF=a-4.作BH⊥AC,垂足为H,求得a的值即可.
解答 解:如图,延长CA至点G使GA=CD,连接GB,
∵△ABC是等边三角形,
∴AB=CA,∠BAC=∠ACB=60°,
∴∠GAB=∠DCA=120°,
∴在△GBA与△DAC中,$\left\{\begin{array}{l}{GA=DC}\\{∠GAB=∠DCA}\\{AB=CA}\end{array}\right.$,
∴△GBA≌△DAC(SAS),
∴BG=AD,
∵AF+CD=AD,AF+GA=GF,
∴GF=AD,
∴BG=GF.
∴∠GBF=∠GFB.
又∵∠GBA=∠CAD,
∴∠ABE=∠AEB,
∴AB=AE.
设AD=a,则BG=a,AB=AE=a-2,GA=GF-AF=BG-AF=a-4,
又∵∠GAB=120°,
∴作BH⊥AC,垂足为H,
∴AH=$\frac{1}{2}$AB=$\frac{1}{2}$(a-2),BH=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$(a-2),GH=$\frac{1}{2}$a-5,
∵BG2=BH2+GH2,
∴a2=$\frac{3}{4}$(a-2)2+($\frac{1}{2}$a-5)2
求a=7,即AD=7.
故答案是:7.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质以及勾股定理.解题的关键是由条件“AF+CD=AD”作出辅助线.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | a>a÷3 | B. | a2>a | C. | a>-a | D. | a2≥0 |
 如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是( )
如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
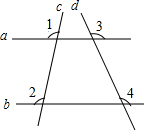 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为110°.
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为110°. 如图,AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,则EF:CD的值为$\frac{1}{4}$.
如图,AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,则EF:CD的值为$\frac{1}{4}$. 如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12.
如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12. 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为(30$\sqrt{2}$+10$\sqrt{6}$)海里.
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为(30$\sqrt{2}$+10$\sqrt{6}$)海里.