题目内容
6. 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为(30$\sqrt{2}$+10$\sqrt{6}$)海里.
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为(30$\sqrt{2}$+10$\sqrt{6}$)海里.
分析 作AD⊥BC于D,根据题意求出∠ABD=45°,得到AD=BD=30$\sqrt{2}$,求出∠C=60°,根据正切的概念求出CD的长,得到答案.
解答 解: 作AD⊥BC于D,
作AD⊥BC于D,
∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,又∠FBC=75°,
∴∠ABD=45°,又AB=60,
∴AD=BD=30$\sqrt{2}$,
∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,
∴∠C=60°,
在Rt△ACD中,∠C=60°,AD=30$\sqrt{2}$,
则tanC=$\frac{AD}{CD}$,
∴CD=$\frac{30\sqrt{2}}{\sqrt{3}}$=10$\sqrt{6}$,
∴BC=BD+CD=30$\sqrt{2}$+10$\sqrt{6}$,
故答案为:(30$\sqrt{2}$+10$\sqrt{6}$)海里.
点评 本题考查的是解直角三角形的知识的应用,掌握锐角三角函数的概念、选择正确的三角函数是解题的关键.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7.
如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为7. 如图1,小红家阳台上放置了一个可折叠的晒衣架,如图2是晒衣架的侧面示意图,经测量:OC=OD=126cm,OA=OB=56cm,且AB=32cm,则此时C,D两点间的距离是72cm.
如图1,小红家阳台上放置了一个可折叠的晒衣架,如图2是晒衣架的侧面示意图,经测量:OC=OD=126cm,OA=OB=56cm,且AB=32cm,则此时C,D两点间的距离是72cm.
 如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米.
如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米.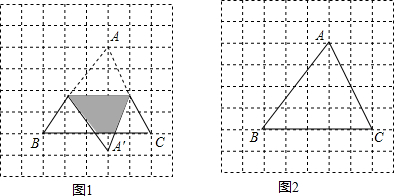
 如图,矩形ABCD是由三个矩形拼接成的,如果AB=8cm,阴影部分的面积是24cm2,另外两个小矩形全等,那么小矩形的长为6cm.
如图,矩形ABCD是由三个矩形拼接成的,如果AB=8cm,阴影部分的面积是24cm2,另外两个小矩形全等,那么小矩形的长为6cm. 如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为$\sqrt{2}$+1.
如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为$\sqrt{2}$+1.