题目内容
5.先化简,再求值:(a-1)÷(a2+1),其中a=$\sqrt{2}$-1.分析 先把a的值代入,再分子和分母分别计算,最后化成最简即可.
解答 解:∵a=$\sqrt{2}$-1
∴(a-1)÷(a2+1)
=$\frac{\sqrt{2}-1-1}{(\sqrt{2}-1)^{2}+1}$
=$\frac{\sqrt{2}-2}{4-2\sqrt{2}}$
=$\frac{\sqrt{2}-2}{-2(\sqrt{2}-2)}$
=-$\frac{1}{2}$.
点评 本题考查了整式的混合运算和求值的应用,解此题的关键是能运用整式的性质进行化简,难度适中.

练习册系列答案
相关题目
20.10:30分,时针与分针的夹角是( )
| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
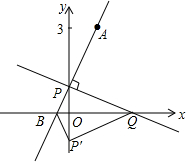 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.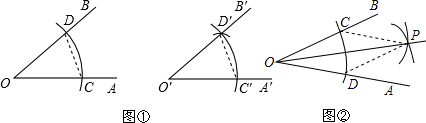
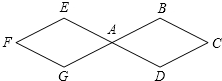 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.