题目内容
7.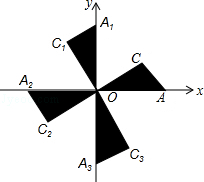 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
分析 根据题意确定出A1,A2,A3,A4…纵坐标,归纳总结得到点A2015的纵坐标与A3纵坐标相同,即可得到结果.
解答 解:∵点A1的坐标为(3,0),OA1=OC2=3,
在Rt△OA2C2中,∠A2OC2=30°,
设A2C2=x,则有OA2=2x,根据勾股定理得:x2+9=4x2,
解得:x=$\sqrt{3}$,即OA2=2$\sqrt{3}$,
∴A2纵坐标为2$\sqrt{3}$,
由OA2=OC3=2$\sqrt{3}$,
在Rt△OA3C3中,∠A3OC3=30°,
设A3C3=y,则有OA3=2y,根据勾股定理得:y2+12=4y2,
解得:y=2,即OA3=4,
∴A3纵坐标为0,
∵2015÷4=503…3,
∴点A2015的纵坐标与A3纵坐标相同,为-3×($\frac{2\sqrt{3}}{3}$)2015.
故选:B.
点评 此题考查了规律型:点的坐标,判断出点A2015的纵坐标与A3纵坐标相同是解本题的关键.

练习册系列答案
相关题目
 如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).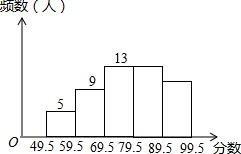 某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.
某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.