题目内容
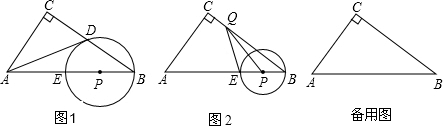
15.(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下列两题:
①如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,则DE=10.
②如图4,在△ABC中,∠BAC=45°,AD⊥BC,且 BD=2,AD=6,求△ABC的面积.
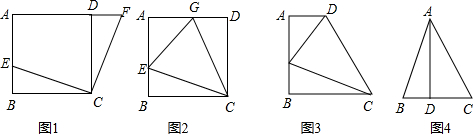
分析 (1)根据正方形的性质,可直接证明△CBE≌△CDF,从而得出CE=CF;
(2)延长AD至F,使DF=BE,连接CF,根据(1)知∠BCE=∠DCF,即可证明∠ECF=∠BCD=90°,根据∠GCE=45°,得∠GCF=∠GCE=45°,利用全等三角形的判定方法得出△ECG≌△FCG,即GE=GF,即可得出答案GE=DF+GD=BE+GD;
(3)①过C作CF⊥AD的延长线于点F.则四边形ABCF是正方形,设DF=x,则AD=12-x,根据(2)可得:DE=BE+DF=4+x,在直角△ADE中利用勾股定理即可求解;
②作∠EAB=∠BAD,∠GAC=∠DAC,过B作AE的垂线,垂足是E,过C作AG的垂线,垂足是G,BE和GC相交于点F,BF=6-2=4,设GC=x,则CD=GC=x,FC=6-x,BC=2+x.在直角△BCF中利用勾股定理求得CD的长,则三角形的面积即可求解.
解答 解:(1)证明:如图1,在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF,
∴CE=CF;
(2)证明:如图2,延长AD至F,使DF=BE,连接CF,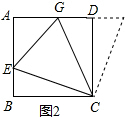
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG,
∴GE=GF,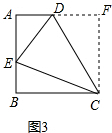
∴GE=DF+GD=BE+GD;
(3)①过C作CF⊥AD的延长线于点F.则四边形ABCF是正方形.
AE=AB-BE=12-4=8,
设DF=x,则AD=12-x,
根据(2)可得:DE=BE+DF=4+x,
在直角△ADE中,AE2+AD2=DE2,则82+(12-x)2=(4+x)2,
解得:x=6.
则DE=4+6=10.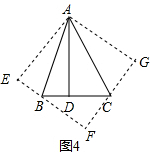
故答案是:10;
②作∠EAB=∠BAD,∠GAC=∠DAC,过B作AE的垂线,垂足是E,过C作AG的垂线,垂足是G,
BE和GC相交于点F,
则四边形AEFG是正方形,且边长=AD=6,BE=BD=2,
则BF=6-2=4,设GC=x,则CD=GC=x,FC=6-x,BC=2+x.
在直角△BCF中,BC2=BF2+FC2,
则(2+x)2=42+x2,
解得:x=3.
则BC=2+3=5,
则△ABC的面积是:$\frac{1}{2}$AD•BC=$\frac{1}{2}$×6×5=15.
点评 本题考查了全等三角形的判定和性质以及正方形的性质,解决本题的关键是注意每个题目之间的关系,正确作出辅助线.

 通城学典默写能手系列答案
通城学典默写能手系列答案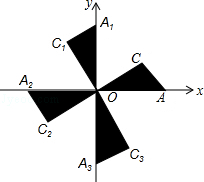 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
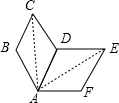 如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )| A. | ∠BAD | B. | ∠CAE | C. | ∠DAF | D. | ∠CAF |