题目内容
19.把直线y=-2x向上平移后得到直线a,直线a经过点(m,n),且2m+n=3,则直线a的解析式是y=-2x+3.分析 根据平移规律“上加下减”得到直线a的解析式,然后根据已知条件列出关于m、n的方程组,通过解方程组求得系数的值.
解答 解:设直线y=-2x向上平移后得到直线a,则直线a的解析式可设为y=-2x+k,
把点(m,n)代入得n=-2m+k,则
$\left\{\begin{array}{l}{n=-2m+k}\\{2m+n=3}\end{array}\right.$,
解得 k=3.
∴直线a的解析式可设为y=-2x+3.
故答案是:y=-2x+3.
点评 本题考查了一次函数图象与几何变换:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当直线平移时k不变,当向上平移m个单位,则平移后直线的解析式为y=kx+b+m.

练习册系列答案
相关题目
9.-$\frac{1}{3}$的相反数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
7.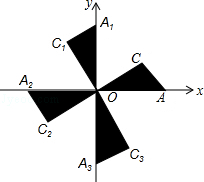 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
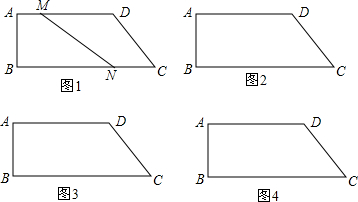
4.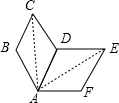 如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
 如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )| A. | ∠BAD | B. | ∠CAE | C. | ∠DAF | D. | ∠CAF |
8.一次函数y=kx+b图象过点(x1,y1)和(x2,y2),且k<0,b<0,当x1<0<x2时,有( )
| A. | y1>y2>b | B. | y2>b>y1 | C. | y2>0>y1 | D. | y1>b>y2 |
 已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.
已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.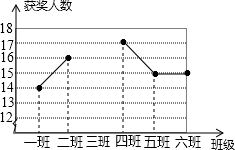 某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作成如图所示不完整的折线统计图. 作图:如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.画出旋转后的△AB′C′.
作图:如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.画出旋转后的△AB′C′.