题目内容
17.某商店从厂家以每件20元的价格购进一批商品,若每件商品售价为a元,预计可卖出(420-12a)件,物价局限定每件商品的加价不得超过进价的20%,如果商店想赚528元,售价应定为多少?分析 可根据关键语“若每件售价a元,则每件盈利(a-20)元,则可卖出(420-12a)件”,根据每件的盈利×销售的件数=获利,即可列出方程求解.
解答 解:设售价应定为a元,
则(a-20)(420-12a)=528,
整理得a2-55a+1228=0,
解得a1=24,a2=31,
∵20(1+20%)=24,而31>22.5
∴a=24.
答:售价应定为24元.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意:判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
相关题目
2.为了了解某校学生的课外阅读情况,随机抽查了10学生周阅读用时数,结果如下表:
则关于这10名学生周阅读所用时间,下列说法正确的是( )
| 周阅读用时数(小时) | 4 | 5 | 8 | 12 |
| 学生人数(人) | 3 | 4 | 2 | 1 |
| A. | 中位数是6.5 | B. | 众数是12 | C. | 平均数是3.9 | D. | 方差是6 |
9.-$\frac{1}{3}$的相反数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
7.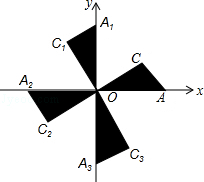 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
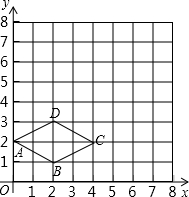 如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.
如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.