题目内容
1.(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为AD=AB+DC;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
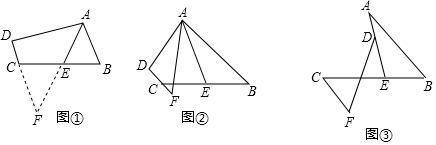
分析 (1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明;
(3)延长AE交CF的延长线于点G,根据相似三角形的判定定理得到△AEB∽△GEC,根据相似三角形的性质得到AB=$\frac{2}{3}$CG,计算即可.
解答 解:(1)如图①,延长AE交DC的延长线于点F,
∵AB∥DC,
∴∠BAF=∠F,
∵E是BC的中点,
∴CE=BE,
在△AEB和△FEC中,
$\left\{\begin{array}{l}{∠BAF=∠F}\\{∠AEB=∠FEC}\\{BE=CE}\end{array}\right.$,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAD的平分线,
∴∠DAF=∠BAF,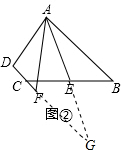
∴∠DAF=∠F,
∴DF=AD,
∴AD=DC+CF=DC+AB,
故答案为:AD=AB+DC;
(2)AB=AF+CF,
证明:如图②,延长AE交DF的延长线于点G,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G,
在△AEB和△GEC中,
$\left\{\begin{array}{l}{∠BAE=∠G}\\{∠AEB=∠GEC}\\{BE=CE}\end{array}\right.$,
∴△AEB≌△GEC,
∴AB=GC,
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG,
∵AB∥CD,
∴∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,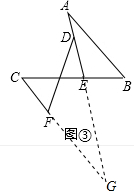
∴AB=CG=AF+CF;
(3)AB=$\frac{2}{3}$(CF+DF),
证明:如图③,延长AE交CF的延长线于点G,
∵AB∥CF,
∴△AEB∽△GEC,
∴$\frac{AB}{CG}$=$\frac{BE}{EC}$=$\frac{2}{3}$,即AB=$\frac{2}{3}$CG,
∵AB∥CF,
∴∠A=∠G,
∵∠EDF=∠BAE,
∴∠FDG=∠G,
∴FD=FG,
∴AB=$\frac{2}{3}$CG=$\frac{2}{3}$(CF+DF).
点评 本题考查的是全等三角形的判定和性质、相似三角形的判定和性质,正确作出辅助性、灵活运用相关的性质定理和判定定理是解题的关键.

| A. | 50° | B. | 100° | C. | 30° | D. | 60° |
| A. | 2×3×52×72 | B. | 2×32×5×72 | C. | 22×3×52×7 | D. | 22×32×5×7 |
| A. | y=2x-1 | B. | y=2x+2 | C. | y=2x-2 | D. | y=2x+1 |
| 时刻 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 |
| 水位高度(米) | 5 | 5.3 | 5.6 | 5.9 | 6.2 |
(1)若水位按照以上上涨规律,当日14:00时,水位高度为6.5米,此时x=5小时;
(2)试写出一个符合表中数据的y关于x的函数关系式;
(3)该水库的最高警戒水位是7米,据统计,这祌上涨规律还会持续3个多小时,当时13:00时,驻地距离水库72千米远的武警官兵接到水库管理员的报警求救电话,防汛指挥部要求武警官兵必须在水库水位到警戒水位武警官兵接到电话后,立即从驻地出发,则他们赶往水库的速度需要什么条件?
 如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.
如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.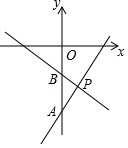 如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.