题目内容
17.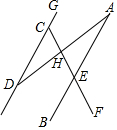 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )| A. | ∠BAD=∠ADG | B. | ∠GCE=∠AEF | C. | ∠GDH+∠DHF=180° | D. | ∠FEB+∠GCE=180° |
分析 根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,进行判断即可.
解答 解;根据∠BAD=∠ADG,可得AB∥CD,故A选项能判定;
根据∠GCE=∠AEF,可得AB∥CD,故B选项能判定;
根据∠GDH+∠DHF=180°,不能得到AB∥CD,故C选项不能判定;
根据∠FEB+∠GCE=180°,∠FEB=∠AEC,可得∠AEC+∠GCE=180°,进而得到AB∥CD,故D选项能判定;
故选:C.
点评 本题主要考查了平行线的判定,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.为了促进我县教研室提出的“悦读悦写”活动的开展,某校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1500人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有300人.
| 每周课外阅读时间(小时) | 0~1 | 1~2(不含1) | 2~3(不含2) | 超过3 |
| 人 数 | 7 | 10 | 14 | 19 |
8.下列等式成立的是( )
| A. | $\frac{1}{2}$=$\frac{b}{2b}$ | B. | $\frac{b}{2b}$=$\frac{1}{2}$ | C. | $\frac{m}{2a}$-$\frac{n}{a}$=$\frac{m-n}{a}$ | D. | a÷b•$\frac{1}{b}$=a |
5. 如图,直线l与x轴、y轴交于点A、B,点C为线段AB上的一动点,过点C分别作CE⊥x轴于点E,作CF⊥y轴于点F.若四边形OECF的周长为6,则直线l的表达式为( )
如图,直线l与x轴、y轴交于点A、B,点C为线段AB上的一动点,过点C分别作CE⊥x轴于点E,作CF⊥y轴于点F.若四边形OECF的周长为6,则直线l的表达式为( )
 如图,直线l与x轴、y轴交于点A、B,点C为线段AB上的一动点,过点C分别作CE⊥x轴于点E,作CF⊥y轴于点F.若四边形OECF的周长为6,则直线l的表达式为( )
如图,直线l与x轴、y轴交于点A、B,点C为线段AB上的一动点,过点C分别作CE⊥x轴于点E,作CF⊥y轴于点F.若四边形OECF的周长为6,则直线l的表达式为( )| A. | y=-x+6 | B. | y=x+6 | C. | y=-x+3 | D. | y=x+3 |
2.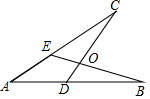 如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )
如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )
 如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )
如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )| A. | ∠B=∠C | B. | BE=CD | C. | AB=AC | D. | ∠CEB=∠BDC |
6.下列选项中所表示的数,哪一个与252的最大公因数为42( )
| A. | 2×3×52×72 | B. | 2×32×5×72 | C. | 22×3×52×7 | D. | 22×32×5×7 |
7.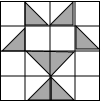 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
 如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.
如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.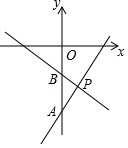 如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.