题目内容
9.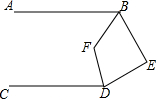 如图,AB∥CD,DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,求∠BFD的度数.
如图,AB∥CD,DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,求∠BFD的度数.
分析 先过E作EG∥AB,根据平行线的性质即可得到∠ABE+∠BED+∠CDE=360°,再根据DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,即可得出∠FBE+∠FDE=135°,最后根据四边形内角和进行计算即可.
解答 解:如图所示,过E作EG∥AB,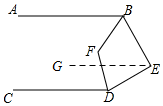
∵AB∥CD,
∴EG∥CD,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠BED+∠CDE=360°,
又∵DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,
∴∠FBE+∠FDE=$\frac{1}{2}$(∠ABE+∠CDE)=$\frac{1}{2}$(360°-90°)=135°,
∴四边形BEDF中,∠BFD=360°-∠FBE-∠FDE-∠BED=360°-135°-90°=135°.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,同旁内角互补.解决问题的关键是作平行线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一张方桌由1个桌面,4个桌腿组成.如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料.那么用多少立方米木料做桌面,多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌?设生产桌面、桌腿的木料分别是x、y立方米,则符合题意的方程是( )
| A. | 50x+300y=1 | B. | 50x+300 y=5 | C. | 50x=1200y | D. | 200x=300y |
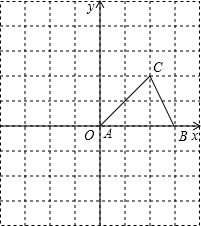 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.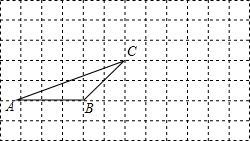 如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: