题目内容
5.求下列各式的值.(1)±$\root{3}{2\frac{10}{27}}$;
(2)-$\root{3}{-\frac{1}{8}}$;
(3)$\sqrt{0.0121}$.
分析 原式利用平方根及立方根定义计算机即可得到结果.
解答 解:(1)原式=±$\root{3}{\frac{64}{27}}$=±$\frac{4}{3}$;
(2)原式=-(-$\frac{1}{2}$)=$\frac{1}{2}$;
(3)原式=0.11.
点评 此题考查了立方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
16.若正比例函数为y=3x,则此正比例函数过(m,6),则m的值为( )
| A. | -2 | B. | 2 | C. | $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
10. 如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
 如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )| A. | AB=DC | B. | OB=OC | C. | ∠A=∠D | D. | ∠AOB=∠DOC |
17.下列各式从左到右的变形正确的是( )
| A. | $\frac{b}{a}=\frac{bc}{ac}$ | B. | $\frac{b}{a}=\frac{b+c}{a+c}$ | C. | $\frac{b}{a}=\frac{b^2}{a^2}$ | D. | $\frac{b}{a}=\frac{ab}{a^2}$ |
14. 如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
 如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )| A. | $\frac{5π}{4}$ | B. | $\frac{5π}{2}$ | C. | 5π | D. | 10π |
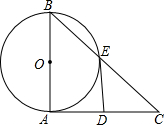 已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,