题目内容
4. 如图,O为坐标原点,⊙O的半径为1,点P是直线y=-2x-6上的动点,过点P作⊙O的切线PA、PB,A、B为切点,连接OA、OB,则四边形OAPB的面积的最小值为$\frac{\sqrt{155}}{5}$.
如图,O为坐标原点,⊙O的半径为1,点P是直线y=-2x-6上的动点,过点P作⊙O的切线PA、PB,A、B为切点,连接OA、OB,则四边形OAPB的面积的最小值为$\frac{\sqrt{155}}{5}$.
分析 可把四边形OAPB转化成Rt△AOP和Rt△BOP,则可知当OP最短时,四边形OAPB的面积最小,设直线交x、y轴于点C、D两点,可知OP最短时为△COD的CD边上的高,由等积法可求得OP的长,可求得答案.
解答 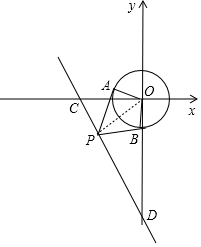 解:
解:
如图,连接OP,设直线y=-2x-6交x轴于点C,交y轴于点C,
∵PA、PB为⊙O的切线,
∴PA=PB,OA⊥PA,OB⊥PB,
∵OA=OB=1,
∴当OP最短时,△AOP和△BOP的面积最小,即四边形OAPB的面积最小,此时OP⊥CD,
在y=-2x-6中,令y=0可求得x=-3,令x=0可求得y=-6,
∴C(-3,0),D(0,-6),
∴OC=3,OD=6,
∴CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴S△COD=$\frac{1}{2}$OC•OD=$\frac{1}{2}$CD•OP,
∴3×6=3$\sqrt{5}$OP,解得OP=$\frac{6\sqrt{5}}{5}$,
在Rt△AOP中,AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=$\frac{\sqrt{155}}{5}$,
∴S四边形OAPB=2S△OAP=2×$\frac{1}{2}$AP•OA=$\frac{\sqrt{155}}{5}$.
故答案为:$\frac{\sqrt{155}}{5}$.
点评 本题主要考查切线的性质,确定出满足条件的P的位置,求得AP的长是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
14. 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )| A. | 9cm | B. | 6cm | C. | 12cm | D. | 3cm |
12.下列各组数中,能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,20 |
19.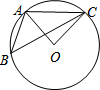 如图,点A、B、C均在⊙O上,若∠ABC=40°,则∠AOC的大小是( )
如图,点A、B、C均在⊙O上,若∠ABC=40°,则∠AOC的大小是( )
 如图,点A、B、C均在⊙O上,若∠ABC=40°,则∠AOC的大小是( )
如图,点A、B、C均在⊙O上,若∠ABC=40°,则∠AOC的大小是( )| A. | 90° | B. | 80° | C. | 70° | D. | 50° |
16.若正比例函数为y=3x,则此正比例函数过(m,6),则m的值为( )
| A. | -2 | B. | 2 | C. | $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
14. 如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
 如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )
如图,已知A、B、C为⊙O上三点,连接BC、AC、OA、OB,若∠ACB=50°,OA=3,则扇形AOB的面积为( )| A. | $\frac{5π}{4}$ | B. | $\frac{5π}{2}$ | C. | 5π | D. | 10π |
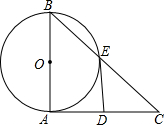 已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,