题目内容
2.(1)解方程组:$\left\{\begin{array}{l}{3x+4y=2}\\{2x-y=5}\end{array}\right.$(2)解不等式组:$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{x-1}{2}≥2x-4}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可.
(2)分别求出两个不等式的解集,求其公共解.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=2①}\\{2x-y=5②}\end{array}\right.$,
②×4+①得:11x=22,即x=2,
把x=2代入②得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{5x+1>3(x-1)①}\\{\frac{x-1}{2}≥2x-4②}\end{array}\right.$
解不等式(1)得:x>-2.
解不等式(2)得:x≤$\frac{7}{3}$.
∴原不等式组的解为-2<x$\frac{7}{3}$.
点评 此题考查了解二元一次方程组和二元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列运算错误是( )
| A. | (a+b)2=a2+b2 | B. | a2•a3=a5 | C. | (a+b)(a-b)=a2-b2 | D. | 3a+4a=7a |
10.有长为8,6,5,3的四根木条,选其中三根构成一个三角形,共可以构成( )个三角形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17.如果一个三角形的两边分别为2和4,则第三边长可能是( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
7.若a>b,则下列不等式一定成立的是( )
| A. | a+1>b+1 | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | -2a>-2b | D. | a+c<b+c |
11.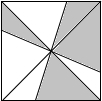 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
 如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( )
如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( ) 如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.
如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.