题目内容
12.解不等式组:$\left\{\begin{array}{l}2x-1>5\\ \frac{3x-7}{2}+1≤x\end{array}\right.$.分析 分别求出两个不等式的解集,求其公共解.
解答 解:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x-7}{2}+1≤x②}\end{array}\right.$
解不等式(1)得:x>3.
解不等式(2)得:x≤5.
∴原不等式组的解为3<x≤5.
点评 本题考查了解一元一次不等式组,求不等式组的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.$\frac{1}{9}$的平方根是( )
| A. | $\frac{1}{3}$ | B. | $±\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $±\frac{1}{81}$ |
1.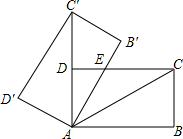 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )| A. | 3 | B. | 1.5 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
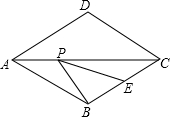 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.