题目内容
3.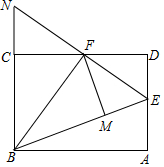 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:①DF=CF;②BF⊥EN;③S△BEF=3S△DEF;④CN=DE.
其中,将正确的结论有几个:( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;易求得BM=2EM=2DE,即可得EB=3EM,根据等高三角形的面积比等于对应底的比,即可求得答案.
解答 解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF.
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF.
∴DF=CF;故①正确.
∵∠BFM=90°-∠EBF,∠BFC=90°-∠CBF,
∴∠BFM=∠BFC.
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN.
∵∠BFE+∠BFN=180°,
∴∠BFE=90°.
即BF⊥EN,故②正确.
在△DEF和△CNF中,
$\left\{\begin{array}{l}{∠D=∠FCN=90°}\\{DF=CF}\\{∠DFE=∠CFN}\end{array}\right.$,
∴△DEF≌△CNF(ASA).
∴EF=FN.
∴BE=BN.
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM.
∴BE=3EM.
∴S△BEF=3S△EMF=3S△DEF;
故③正确.
在△CFN与△DFE中,$\left\{\begin{array}{l}{∠NCF=∠D=90°}\\{∠CF=DF}\\{∠CFN=∠DFE}\end{array}\right.$,
∴△CFN≌△DEF,
∴CN=DE;故④正确.
故选C.
点评 此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
12.若a<2,化简$\sqrt{{{(a-2)}^2}}-3$=( )
| A. | a-5 | B. | 5-a | C. | 1-a | D. | -1-a |
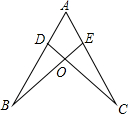 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点、已知AB=AC,BD=CE,求证:∠B=∠C.
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点、已知AB=AC,BD=CE,求证:∠B=∠C.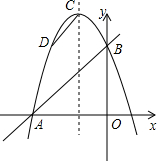 如图,一次函数y=x+3的图象与坐标轴分别交于A,B两点,二次函数y=ax2+bx-3a的图象经过点A,B.
如图,一次函数y=x+3的图象与坐标轴分别交于A,B两点,二次函数y=ax2+bx-3a的图象经过点A,B.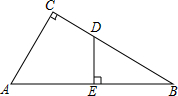 如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.