题目内容
11.解方程(组)(1)$\frac{x+2}{3}$-$\frac{x-1}{2}$=x+1
(2)$\left\{\begin{array}{l}{2x-y=5}\\{x-1=\frac{1}{2}(2y-1)}\end{array}\right.$.
分析 (1)根据解一元一次方程的方法解方程即可;
(2)将两个方程先化简,再选择正确的方法进行消元,本题适合用加减法求解.
解答 解:(1)$\frac{x+2}{3}$-$\frac{x-1}{2}$=x+1
去分母得,2x+4-3x+3=6x+6,
移项并合并得,7x=1,
系数化为1得,x=$\frac{1}{7}$;
(2)化简可得$\left\{\begin{array}{l}{2x-y=5①}\\{2x-2y=1②}\end{array}\right.$,
①-②,得y=4,
把y=4代入①,得2x-4=5,
解得x=4.5.
∴原方程组的解为$\left\{\begin{array}{l}{x=\frac{9}{2}}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,一元一次方程,利用了消元的思想,消元的方法为:加减消元法与代入消元法.

练习册系列答案
相关题目
1.已知一次函数y=ax+b,其中x和y的部分对应值如下表:
那么方程ax+b=0的解是x=1.5.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 7 | 5 | 3 | 1 | -1 | -3 |
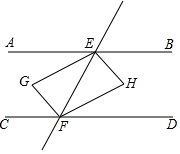 如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.
如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.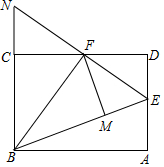 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论: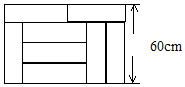 用8块相同的小长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,求小长方形地砖的面积.
用8块相同的小长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,求小长方形地砖的面积.