题目内容
4．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y＜2，求整数a的最大值．分析 先把两式相加求出x+y的值，再代入x+y＜2中得到关于a的不等式，求出a的取值范围，进而求解即可．
解答 解：$\left\{\begin{array}{l}{3x+y=1+a①}\\{x+3y=3②}\end{array}\right.$，
①+②得，x+y=1+$\frac{a}{4}$，
∵x+y＜2，
∴1+$\frac{a}{4}$＜2，
解得a＜4．
故整数a的最大值为3．
点评 本题考查的是解二元一次方程组及解一元一次不等式，解答此题的关键是把a当作已知条件表示出x+y的值，再得到关于a的不等式．
练习册系列答案
相关题目
14．为了保持生态平衡，绿化环境，国家大力鼓励“退耕还林、还草”，其补偿政策如下表．
（1）该去年该农户承包了30亩山坡地种树种草，共得到国家补粮4000千克，则去年种树、种草各多少亩？
（2）若今年该农户增加40亩山坡地种树种草，要想年终政府补钱不少于12000元，至少需要增加安排多少亩山坡地种树？
| 种树、种草每亩每年补粮补钱情况表 | ||
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
（2）若今年该农户增加40亩山坡地种树种草，要想年终政府补钱不少于12000元，至少需要增加安排多少亩山坡地种树？
15．下列四个命题中，正确的是（ ）
| A． | 经过直线外一点，有且只有一条直线与这条直线平行 | |
| B． | 同旁内角相等，两直线平行 | |
| C． | 相等的角是对顶角 | |
| D． | 如果两条直线都与第三条直线垂直，那么这两条直线也互相垂直 |
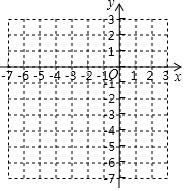如图所示，在平面直角坐标系中有一格点三角形，该三角形的三个顶点为：A（1，1），B（-3，1），C（-3，-1）．
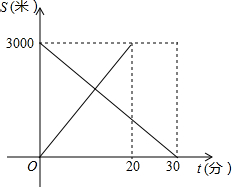甲从A地出发，匀速步行到B地，同时，乙从B地出发，匀速步行到A地，甲乙两人与A地的距离S（米）与出发时间t（分钟）的关系如图：
16．若a的倒数是-1，则a2017的值是（ ）
| A． | 1 | B． | -1 | C． | 2017 | D． | -2017 |
13．下列图形中既是轴对称图形又是中心对称图形的是（ ）
| A． | 等腰三角形 | B． | 等腰梯形 | C． | 平行四边形 | D． | 矩形 |