题目内容
19.甲、乙两列火车从A,B两地相向而行,乙车比甲车早出发1h,甲车比乙车的速度快30km/h,甲车发车2h后与乙车相遇,相遇后,甲车以原速度的$\frac{2}{3}$行驶,乙车以原速度的$\frac{5}{3}$行驶,结果$\frac{9}{4}$h后,两车的距离等于A,B两地间的距离,求两车相遇前的速度和A,B两地之间的距离.分析 设两车相遇前乙车的速度为xkm/h,则甲车的速度为(x+30)km/h,根据路程=速度×时间,即可得出关于x的一元一次方程,解之即可得出x的值,将其代入x+30、3x+2(x+30)中即可求出结论.
解答 解:设两车相遇前乙车的速度为xkm/h,则甲车的速度为(x+30)km/h,
根据题意得:3x+2(x+30)=[$\frac{2}{3}$(x+30)+$\frac{5}{3}$x]×$\frac{9}{4}$,
解得:x=60,
∴x+30=90,3x+2(x+30)=360.
答:两车相遇前甲车的速度为90 km/h,乙车的速度为60 km/h,A、B两地的距离为360 km/h.
点评 本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
14.如果单项式-xa+1y3与12ybx2是同类项,那么a,b的值分别为( )
| A. | a=2,b=3 | B. | a=1,b=2 | C. | a=2,b=2 | D. | a=1,b=3 |
9.下列四个几何体中,从左面看是圆的几何体是( )
| A. | 圆锥 | B. | 正方体 | C. | 球 | D. | 圆柱 |
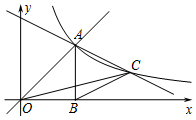 如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.
如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.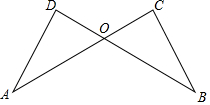 已知:如图,AD=BC,AC=BD.试猜想线段OD与OC数量关系并证明你的猜想.
已知:如图,AD=BC,AC=BD.试猜想线段OD与OC数量关系并证明你的猜想.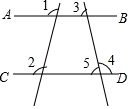 已知∠1=∠2,∠3=70°,求∠4的度数,填空(理由或数学式)
已知∠1=∠2,∠3=70°,求∠4的度数,填空(理由或数学式) 如图,正方形ABCD中,E,F分别为边AD,BC上一点,且∠1=∠2.求证:四边形BFDE是平行四边形.
如图,正方形ABCD中,E,F分别为边AD,BC上一点,且∠1=∠2.求证:四边形BFDE是平行四边形.