题目内容
11.解方程:(1)x2-1=2(x+1)
(2)x2-6x-4=0.
分析 (1)先移项,然后根据提公因式法可以解答此方程;
(2)根据配方法可以解答此方程.
解答 解:(1)x2-1=2(x+1)
(x+1)(x-1)-2(x+1)=0,
(x+1)(x-1-2)=0
(x+1)(x-3)=0,
∴x+1=0或x-3=0,
解得,x1=-1,x2=3;
(2)x2-6x-4=0
x2-6x=4
x2-6x+9=4+9
(x-3)2=13,
∴x-3=$±\sqrt{13}$,
解得,x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$.
点评 本题考查解一元二次方程-因式分解法、配方法,解题的关键是会用因式分解法和配方法解方程.

练习册系列答案
相关题目
2.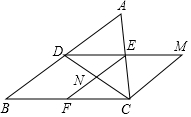 如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
 如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
1.比-2小的数是( )
| A. | -4 | B. | $\frac{1}{2}$ | C. | 0 | D. | -1 |
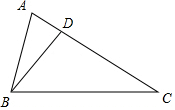 如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比.
如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比. 如图,在△ABC中,D、E分别是AC、AB边上的点,∠AED=∠C,AB=10,AD=6,AC=8,求BE的长.
如图,在△ABC中,D、E分别是AC、AB边上的点,∠AED=∠C,AB=10,AD=6,AC=8,求BE的长.