题目内容
4.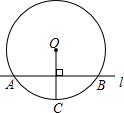 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
分析 连接OA,根据垂径定理求出AD的长,再由勾股定理求出OD的长,进而得出CD的长即可得出结论.
解答  解:连接OA,
解:连接OA,
∵OC=10cm,AB⊥OC,AB=12cm,
∴AD=$\frac{1}{2}$AB=6cm,
∴OD=$\sqrt{{OA}^{2}-{AD}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8(cm),
∴CD=OC-OD=10-8=2cm,
∴直线AB沿OC的方向向下平移2cm时与圆相切.
故选A.
点评 本题考查的是直线与圆的位置关系,熟知直线与圆相切的条件是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
16.2013年入春以来,北方部分地区干旱严重,导致凤凰社区人畜饮用水紧张.每天需从社区外调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点.甲厂每天最多可调出80吨.乙厂每天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运饮用水多少吨?
(2)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(3)怎样安排调运方案才能使每天的总运费最省?
| 到凤凰社区供水点的路程(千米) | 运费(元/吨•千米) | |
| 甲厂 | 20 | 12 |
| 乙厂 | 14 | 15 |
(2)设从甲厂调运饮用水x吨.总运费为w元.试写出w与x的函数关系式.
(3)怎样安排调运方案才能使每天的总运费最省?
13.将抛物线$y=-\frac{1}{2}{x^2}$+2x+1的顶点坐标为( )
| A. | (2,3) | B. | (-2,-3) | C. | (-2,-1) | D. | (2,-3) |
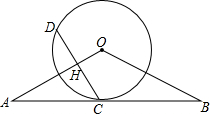 如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E.
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E.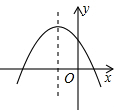 二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )
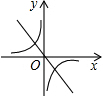
二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )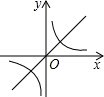

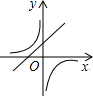

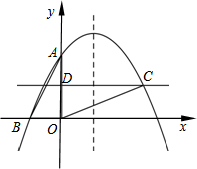 如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.
如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.