题目内容
12.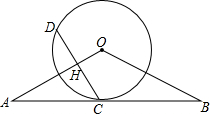 如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E.
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E.(1)证明:直线AB与⊙O相切;
(2)若AE=a,AB=b,求⊙O的半径;(结果用a,b表示)
(3)过点C作弦CD⊥OA于点H,试探究⊙O的直径与OH、OB之间的数量关系,并加以证明.
分析 (1)利用段垂直平分线的性质得出OC⊥AB,进而得出答案即可;
(2)利用勾股定理得出OC2+AC2=OA2,进而得出⊙O的半径;
(3)首先得出△HOC∽△COA,进而得出OC2=OH×OA,即可得出⊙O的直径与OH、OB之间的数量关系.
解答 (1)证明:如图所示:连接CO,
∵OA=OB,AC=BC,
∴OC⊥AB,
∵OC为⊙O的半径,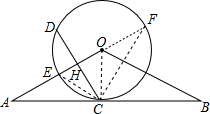
∴直线AB与⊙O相切;
(2)解:在直角三角形OAC中用勾股定理就可以了.设半径为r,则OC=r,OA=a+r,
AC=$\frac{1}{2}$AB=$\frac{1}{2}$b,
在Rt△AOC中,
OC2+AC2=OA2,
则r2+$\frac{1}{4}$b2=(a+r)2,
解得:r=$\frac{{b}^{2}}{8a}$-$\frac{a}{2}$;
(3)d2=4OH×OB,
理由:∵OA⊥CD,OC⊥AC,
∴∠OCA=∠OHC,
∵∠HOC=∠COA,
∴△HOC∽△COA,
∴$\frac{OH}{OC}$=$\frac{OC}{OA}$,
即OC2=OH×OA,
∵OC垂直平分AB,
∴OA=OB,
设直径为d,则OC=$\frac{d}{2}$,
∴($\frac{d}{2}$)2=OH×OB,
即d2=4OH×OB.
点评 此题主要考查了圆的综合以及相似三角形的判定与性质,得出△HOC∽△COA是解题关键.

练习册系列答案
相关题目
10.2014年11月22日,某银行将三年期定期存款的年利率由4.25%下调0.25个百分点,又上浮1.2倍后为4.8%,某客户11月23日在该银行存入三年期定期存款若干,到期后所得利息将比利率调整前存入所得利息多891元.则该客户存入该银行的本金为( )
| A. | 4.8万元 | B. | 5.2万元 | C. | 5.4万元 | D. | 5.8万元 |
17.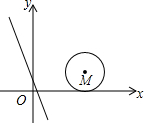 如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
 如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )| A. | 1+$\sqrt{5}$或1+2$\sqrt{5}$ | B. | 1+2$\sqrt{5}$或1+4$\sqrt{5}$ | C. | 9+2$\sqrt{5}$或9-2$\sqrt{5}$ | D. | 10+2$\sqrt{5}$或10-2$\sqrt{5}$ |
4.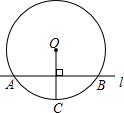 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
2.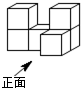 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )| A. | 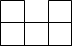 | B. | 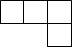 | C. | 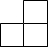 | D. |  |
 如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.
如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.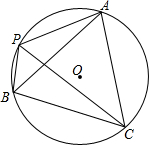 如图:已知AB=AC,∠APC=60°.
如图:已知AB=AC,∠APC=60°. 如图,长方体的长、宽、高分别为8、4、5,一只蚂蚁沿长方体表面从顶点A爬到顶点B,则它走过的路程最短为$\sqrt{145}$.
如图,长方体的长、宽、高分别为8、4、5,一只蚂蚁沿长方体表面从顶点A爬到顶点B,则它走过的路程最短为$\sqrt{145}$.