题目内容
4.某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利50元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当降价措施,经调查发现,如果每件衬衫降价5元,商场平均每天可多销售出10件.(1)若商场每件降价5元,问商场每天可盈利多少元?
(2)若商场平均每天要盈利1600元,且让顾客尽可能多得实惠,每件衬衫应降价多少元?
(3)要使商场平均每天盈利2000元,可能吗?请说明理由.
分析 (1)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润直接求解即可;
(2)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可;
(3)同样列出方程,若方程有实数根则可以,否则不可以.
解答 解:(1)设每件衬衫应降价x元.
根据题意,得总利润y=(50-x)(20+2x)
令x=5,得到y=45×30=1350元,
答:降价5元可以盈利1350元;
(2)令y=(50-x)(20+2x)=1600
整理,得x2-40x+300=0
解得x1=10,x2=30.
∵“扩大销售量,减少库存”,
∴x1=10应略去,
∴x=30.
答:每件衬衫应降价30元;
(3)令y=(50-x)(20+2x)=2000,
整理,得x2-40x+500=0
∵△=1600-4×500<0,
∴商场平均每天不可能盈利2000元.
点评 此题主要考查了一元二次方程的应用,利用基本数量关系:平均每天售出的件数×每件盈利=每天销售的利润是解题关键.

练习册系列答案
相关题目
4.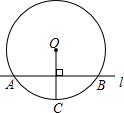 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
 如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.
如图,AB⊥CD,垂足为O,EF过点O,OM⊥EF,已知∠AOM=2∠FOD,求∠FOD的度数.