题目内容
在Rt△ABC中，CD是斜边AB上的高，已知BC=| 7 |
| 3 |
考点：锐角三角函数的定义,勾股定理
专题：
分析：在直角△BCD中利用勾股定理求得CD的长，然后证明∠A=∠BCD，即可求解．
解答：解：在直角△BCD中，CD=
=
=2，
∵Rt△ABC中，CD是斜边AB上的高，
∴∠A=∠BCD，
则tan∠A=tan∠BCD=
=
．
故答案是：
．
| BC2-BD2 |
| 7-3 |
∵Rt△ABC中，CD是斜边AB上的高，
∴∠A=∠BCD，
则tan∠A=tan∠BCD=
| BD |
| CD |
| ||
| 2 |
故答案是：
| ||
| 2 |
点评：本题考查了锐角三角函数，以及勾股定理，正确理解锐角三角函数的定义是关键．
练习册系列答案
相关题目
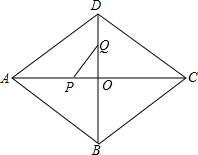如图，在菱形ABCD中，AC、BD交于点O，AD=15，AO=12．动点P以每秒2个单位的速度从点A出发，沿AC向点C匀速运动．同时，动点Q以每秒1个单位的速度从点D出发，沿DB向点B匀速运动．当其中有一点到达终点时，另一点也停止运动．设运动的时间为t秒．在△ABC中，∠C=90°，若c=29，a=20，则b=（ ）
| A、9 | B、10 | C、20 | D、21 |