题目内容
20. 如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.
如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.
分析 由△AOP的面积可求得P点纵坐标,再求得直线AB解析式,可求出P点坐标,再把P点坐标代入抛物线解析式可求得a的值.
解答 解:
∵A(4,0),
∴OA=4,
设P点纵坐标为y(y<0),
∴S△AOP=$\frac{1}{2}$OA•|(-y),
即$\frac{1}{2}$×4(-y)=$\frac{19}{2}$,解得y=-$\frac{19}{4}$,
设直线AB解析式为y=kx+b,
把A、B坐标代入可得$\left\{\begin{array}{l}{4k+b=0}\\{b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$,
∴直线AB解析式为y=x-4,
∵P点也在直线AB上,
∴-$\frac{19}{4}$=x-4,解得x=-$\frac{3}{4}$,
∵P点在抛物线上,
∴-$\frac{19}{4}$=a(-$\frac{3}{4}$)2,解得a=-$\frac{76}{9}$.
点评 本题主要考查函数的交点问题,掌握函数图象的交点坐标满足每一个函数解析式是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.下列各对数中,互为相反数的是( )
| A. | -(-3)和-|-3| | B. | |-2|和|2| | C. | -(-1)和|-1| | D. | |m|与|-m| |
 已知△ABC,∠A=60°,BC=6.
已知△ABC,∠A=60°,BC=6.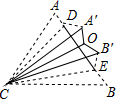 如图,已知△ABC是等边三角形,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
如图,已知△ABC是等边三角形,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )