题目内容
15.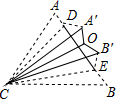 如图,已知△ABC是等边三角形,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
如图,已知△ABC是等边三角形,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )| A. | 120° | B. | 135° | C. | 140° | D. | 150° |
分析 由翻折的性质得:∠ACD=∠DCA′=∠A′CO,∠BCE=∠ECB′=∠B′CO,故∠A′CB′=$\frac{1}{3}$∠ACB,代入数值即可.
解答 解:由翻折的性质得:∠ACD=∠DCA′=∠A′CO,∠BCE=∠ECB′=∠B′CO,
∴∠A′CB′=$\frac{1}{3}$∠ACB=$\frac{1}{3}$×60°=20°,
∴∠A′OB′的度数=140°
故选C
点评 本题主要考查了翻折的性质,能灵活应用翻折的性质是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
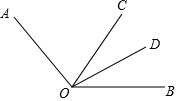 如图,已知∠AOC=80°,∠BOC=50°,OD平分∠BOC,求∠AOD.
如图,已知∠AOC=80°,∠BOC=50°,OD平分∠BOC,求∠AOD. 如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.
如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.