题目内容
10. 已知△ABC,∠A=60°,BC=6.
已知△ABC,∠A=60°,BC=6.(1)求作△ABC的外接圆.
(2)求∠BOC的度数.
(3)求⊙O的半径.
分析 (1)画出边AC,AB的垂直平分线,两线交于一点O,以O为圆心,OB长为半径画圆即可;
(2)由圆周角定理即可求出∠BOC的度数;
(3)过点O作OD⊥BC于点D,即可得出CD的长以及∠COD的度数,进而利用锐角三角函数关系求出即可.
解答 解:(1)如图所示:⊙O即为所求△ABC的外接圆;
(2)∵∠A=60°,
∴∠BOC=2∠A-120°;
(3)过点O作OD⊥BC于点D,
∵∠A=60°,BC=6,
∴∠COD=60°,CD=$\frac{1}{2}$BC=3,
∴sin∠COD=$\frac{CD}{OC}$,
∴OC=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$.
即⊙O的半径为2$\sqrt{3}$.
点评 此题主要考查了作三角形的外接圆以及锐角三角函数关系应用,解题的关键是正确找到圆心所在位置.

练习册系列答案
相关题目
18.在△ABC中,∠C=90°,AC=3,CB=4,则cotA的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
5.在分数$\frac{1}{4}$,$\frac{15}{20}$,$\frac{9}{12}$,$\frac{3}{4}$,$\frac{25}{100}$,$\frac{75}{100}$中,与$\frac{18}{24}$相等的分数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.我省从2010年7月开始实施阶梯电价制,居民生活用电价格方案如下表:
例:若某用户2010年8月份的用电量为300度,则需缴交电费为:200×0.5+(300-200)×0.55=155(元).
(1)填空:如果小华家2010年9月份的用电量为100度,则需缴交电费50元;
(2)如果小华家2010年10月份的用电量为a度(其中200<a≤400),则需缴交电费多少元?(用含a的代数式表示,并化简)
(3)如果小华家2010年11、12两个月共用电700度(其中12月份的用电量达到“第3档”),设11月份的用电量为b度,则小华家这两个月共需缴交电费多少元?(用含b的代数式表示,并化简)
| 档次 | 月用电量 | 电价(单位:元/度) |
| 第1档 | 月用电量≤200度 | 0.5 |
| 第2档 | 200度<月用电量≤400度 | 0.55 |
| 第3档 | 月用电量>400度 | 0.8 |
(1)填空:如果小华家2010年9月份的用电量为100度,则需缴交电费50元;
(2)如果小华家2010年10月份的用电量为a度(其中200<a≤400),则需缴交电费多少元?(用含a的代数式表示,并化简)
(3)如果小华家2010年11、12两个月共用电700度(其中12月份的用电量达到“第3档”),设11月份的用电量为b度,则小华家这两个月共需缴交电费多少元?(用含b的代数式表示,并化简)
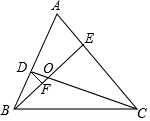 已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.
已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.
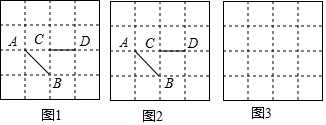
 如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.
如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.