题目内容
 如图,将△ABC纸片沿DE折叠,当点A落在四边形BCDE外部(即图中的A′)时,∠A与∠1、∠2之间始终满足的数量关系是
如图,将△ABC纸片沿DE折叠,当点A落在四边形BCDE外部(即图中的A′)时,∠A与∠1、∠2之间始终满足的数量关系是考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:根据折叠的性质可得∠A′=∠A,根据平角等于180°用∠2表示出∠AEA′,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠1与∠A′表示出∠3,然后利用三角形的内角和等于180°列式整理即可得解.
解答: 解:∵△A′DE是△ADE沿DE折叠得到,
解:∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,
∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°,
整理得,2∠A=∠2-∠1.
∴∠A=
(∠1-∠2).
故答案为:∠A=
(∠1-∠2).
 解:∵△A′DE是△ADE沿DE折叠得到,
解:∵△A′DE是△ADE沿DE折叠得到,∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,
∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°,
整理得,2∠A=∠2-∠1.
∴∠A=
| 1 |
| 2 |
故答案为:∠A=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理以及折叠的性质,根据折叠的性质,平角的定义以及三角形的一个外角等于与它不相邻的两个内角的和的性质把∠1、∠2、∠A转化到同一个三角形中是解题的关键.

练习册系列答案
相关题目
若代数式
与
x+5的值互为相反数,则x的值为( )
| x-8 |
| 3 |
| 1 |
| 4 |
| A、-4 | ||
| B、92 | ||
| C、4 | ||
D、
|
 如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为
如图,在等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为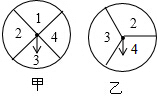 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5).
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5).