题目内容
已知a、b、c均为实数，且
+|b-4|+（c+5）2=0，求方程ax2+bx+c=0的解．
| a-2 |
考点：解一元二次方程-公式法,非负数的性质：绝对值,非负数的性质：偶次方,非负数的性质：算术平方根
专题：计算题
分析：利用非负数的性质求出a，b，c的值，代入方程计算即可求出解．
解答：解：∵
+|b-4|+（c+5）2=0，
∴a=2，b=4，c=-5，
代入方程得：2x2+4x-5=0，
这里a=2，b=4，c=-5，
∵△=16+40=56，
∴x=
=
．
| a-2 |
∴a=2，b=4，c=-5，
代入方程得：2x2+4x-5=0，
这里a=2，b=4，c=-5，
∵△=16+40=56，
∴x=
-4±2
| ||
| 4 |
-2±
| ||
| 2 |
点评：此题考查了解一元二次方程-公式法，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
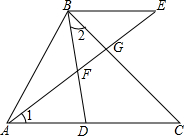如图，D是AC上一点，BE∥AC，AE分别交BD，BC于点F，G．若∠1=∠2，线段BF，FG，FE之间有怎样的关系？请说明理由．
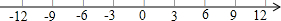已知点P，Q是数轴上的两个动点，且P，Q两点的速度比是3：5．（速度单位：单位长度/秒）