题目内容
3．数据：3，4，3，5，6中，众数和中位数分别为（ ）| A． | 3，3 | B． | 2，3 | C． | 3，4 | D． | 3，3.5 |
分析 将数据按照从小到大依次排列为3，3，4，5，6，根据众数和中位数的定义解答．
解答 解：将数据按照从小到大依次排列为3，3，4，5，6，
可见，出现次数最多的数为3，故众数为3；处在中间位置的数为4，中位数为4．
故选C．
点评 本题考查了众数和中位数，熟悉它们的定义是解题的关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
13．有8张卡片，分别写着1、2、3、4、4、3、6、5的大小完全相同的数字卡片，将它们背面朝上洗均匀后任意抽出一张，结果抽到数字3的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{8}$ | D． | $\frac{5}{8}$ |
在平面直角坐标系xOy中，直线y=x-1与y轴交于点A，与双曲线y=$\frac{k}{x}$交于点B（m，2）．
18．
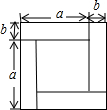如图，将完全相同的四个长方形纸片拼成一个大的正方形，用两种不同的方法表示这个大正方形的面积，则可以得出一个等式为（ ）
如图，将完全相同的四个长方形纸片拼成一个大的正方形，用两种不同的方法表示这个大正方形的面积，则可以得出一个等式为（ ）| A． | （a+b）2=a2+2ab+b2 | B． | （a-b）2=a2-2ab+b2 | C． | a2-b2=（a+b）（a-b） | D． | （a+b）2=（a-b）2+4ab |
8．关于x的一元二次方程x2-6x+k=0有两个不相等的实数根，则实数k的取值范围是（ ）
| A． | k≤9 | B． | k＜9 | C． | k≥9 | D． | k＞9 |
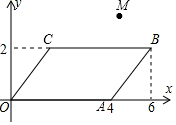如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，且A（4，0）、B（6，2）、M（4，3）．在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分，请写出该直线的函数表达式y=2x-5．
12．
某学校拟建一间矩形活动室，一面靠墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门，已知计划中的材料可建墙体（不包括门）总长为27m，建成后的活动室面积为75m2，求矩形活动室的长和宽，若设矩形宽为x，根据题意可列方程为（ ）
某学校拟建一间矩形活动室，一面靠墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门，已知计划中的材料可建墙体（不包括门）总长为27m，建成后的活动室面积为75m2，求矩形活动室的长和宽，若设矩形宽为x，根据题意可列方程为（ ）| A． | x（27-3x）=75 | B． | x（3x-27）=75 | C． | x（30-3x）=75 | D． | x（3x-30）=75 |
13．
如图，直线a∥b，直线c分别与a，b相交于A，C两点，AC⊥AB于点A，AB交直线b于点B，若∠1=40°，则∠ABC的度数为（ ）
如图，直线a∥b，直线c分别与a，b相交于A，C两点，AC⊥AB于点A，AB交直线b于点B，若∠1=40°，则∠ABC的度数为（ ）| A． | 52° | B． | 50° | C． | 45° | D． | 40° |