题目内容
14.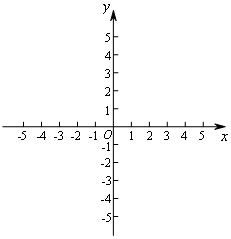 在平面直角坐标系xOy中,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2).
在平面直角坐标系xOy中,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2).(1)求点B的坐标及k的值;
(2)将直线AB平移后与x轴交于点C,若S△ABC=6,求点C的坐标.
分析 (1)利用待定系数法即可解决问题;
(2)直线y=x-1与y轴交于点A,可得A(0,-1).设直线y=x-1与x轴交于点D,则D(1,0).根据S△ABC=S△CDB+S△CDA=6,列出方程求出CD即可解决问题.
解答 解:(1)把B(m,2)代入y=x-1中得,m=3.
则B(3,2),
∵B(3,2)在双曲线y=$\frac{k}{x}$的图象上,
∴k=6.
(2)∵直线y=x-1与y轴交于点A,
∴A(0,-1).
设直线y=x-1与x轴交于点D,
则D(1,0).
∵S△ABC=S△CDB+S△CDA=6,
∴$\frac{1}{2}$•CD•2+$\frac{1}{2}$•CD•1=6,
解得,CD=4.
∵D(1,0),
∴C(5,0),C′(-3,0).
点评 本题考查反比例函数与一次函数的交点问题、三角形的面积等知识,解题的关键是熟练掌握待定系数法,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如果分式$\frac{{{m^2}-4}}{m-2}$的值为零,那么m的值是( )
| A. | m≠2 | B. | m=±2 | C. | m=-2 | D. | m=2 |
19.按如图所示的程序计算,若开始输入n的值为1,则最后输出的结果是( )

| A. | 3 | B. | 42 | C. | 15 | D. | 63 |
3.数据:3,4,3,5,6中,众数和中位数分别为( )
| A. | 3,3 | B. | 2,3 | C. | 3,4 | D. | 3,3.5 |
4. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )| A. | AD=AB | B. | ∠D+∠BOC=90° | C. | ∠BOC=2∠D | D. | ∠D=∠B |
 如图,按此规律,第30行最后一个数是88.
如图,按此规律,第30行最后一个数是88.