题目内容
14.解三元一次方程组$\left\{\begin{array}{l}{x+3y+2z=10①}\\{2x+y+z=7②}\\{-x+2y+3z=12③}\end{array}\right.$应先消去未知数x,得到关于y、z的二元一次方程组$\left\{\begin{array}{l}{5y+5Z=22}\\{5y+7z=31}\end{array}\right.$,解这个二元一次方程组得$\left\{\begin{array}{l}{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$,原方程组的解是$\left\{\begin{array}{l}{x=\frac{13}{10}}\\{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$.分析 先消去x,转化为关于y、z的二元方程组即可解决.
解答 解:$\left\{\begin{array}{l}{x+3y+2z=10}&{①}\\{2x+y+z=7}&{②}\\{-x+2y+3z=12}&{③}\end{array}\right.$
①+③得到:5y+5z=22 ④
②+2×③得到:5y+7z=31 ⑤
由④⑤得$\left\{\begin{array}{l}{5y+5z=21}\\{5y+7z=31}\end{array}\right.$解得$\left\{\begin{array}{l}{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$代入②得x=$\frac{13}{10}$,$\left\{\begin{array}{l}{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$
∴$\left\{\begin{array}{l}{x=\frac{13}{10}}\\{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$.
故答案分别为x;y、z;$\left\{\begin{array}{l}{5y+5z=22}\\{5y+7z=31}\end{array}\right.$;$\left\{\begin{array}{l}{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$;$\left\{\begin{array}{l}{x=\frac{13}{10}}\\{y=-\frac{1}{10}}\\{z=\frac{9}{2}}\end{array}\right.$.
点评 本题考查三元方程组,解题的关键是三元方程组转化为二元方程组,学会转化的数学思想,属于中考常考题型.

| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
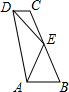 已知:如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE.求证:AD=AB+CD.
已知:如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE.求证:AD=AB+CD. 如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形.
如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形. 如图,△ABC是等边三角形,边长为4,则C点的坐标是(2$\sqrt{3}$,-2).
如图,△ABC是等边三角形,边长为4,则C点的坐标是(2$\sqrt{3}$,-2).